What is Advent of Code?
Advent of Code is a 25-day coding challenge leading up to Christmas. The creator of the challenge, Eric Wastl, describes it as "an Advent calendar of small programming puzzles for a variety of skill sets and skill levels that can be solved in any programming language you like. People use them as a speed contest, interview prep, company training, university coursework, practice problems, or to challenge each other."
I started the challenge at the beginning of December. It was brought to my attention by some other members of the Pitt CSC Discord, and after looking into it I discovered it to be a great way to keep technical interview skills fresh in my mind. Each puzzle follows a similar format, yet addresses different skills and different problem solving techniques. The problems also cover various difficulty levels, and it's not always necessary to complete one day's problem to do the next. It is cool to complete the problems sequentially, however, since there's a goofy, fantastical storyline associated with the problems to make them more engaging.
The goal of the challenge is to complete all 25 problems and obtain 50 stars (25 days x 2 parts to each puzzle). At the time of me writing this blog, I only have been able to collect 13 stars, mostly because as soon as I got really into the challenge, finals came up behind me and diverted my focus. However, I will continue to work on the problems when I can and hopefully update this post as I get further along through the challenge. (Here's a git repo containing my solutions up to the current point in time) That's the beauty of the website, it's still up after December! So this is a great way for preparing for interviews or challenging yourself even not during the Christmas season.
Further, they've been releasing these ever since 2015, so that means the website has 175 total coding problems you could hypothetically complete. None of it has to be done in order too! I would highly recommend checking out the website at the link above if you haven't already. If you're interested in more information, I will be giving a more in-depth look of the first problem from 2021 and how I went about solving it.
Problem Description
Let's start by exploring the problem released for December 1st. The post in it's entirety can be found here. I will only be looking at Part 1. If you complete Part 1 using the assistance of this guide, try Part 2 on your own!
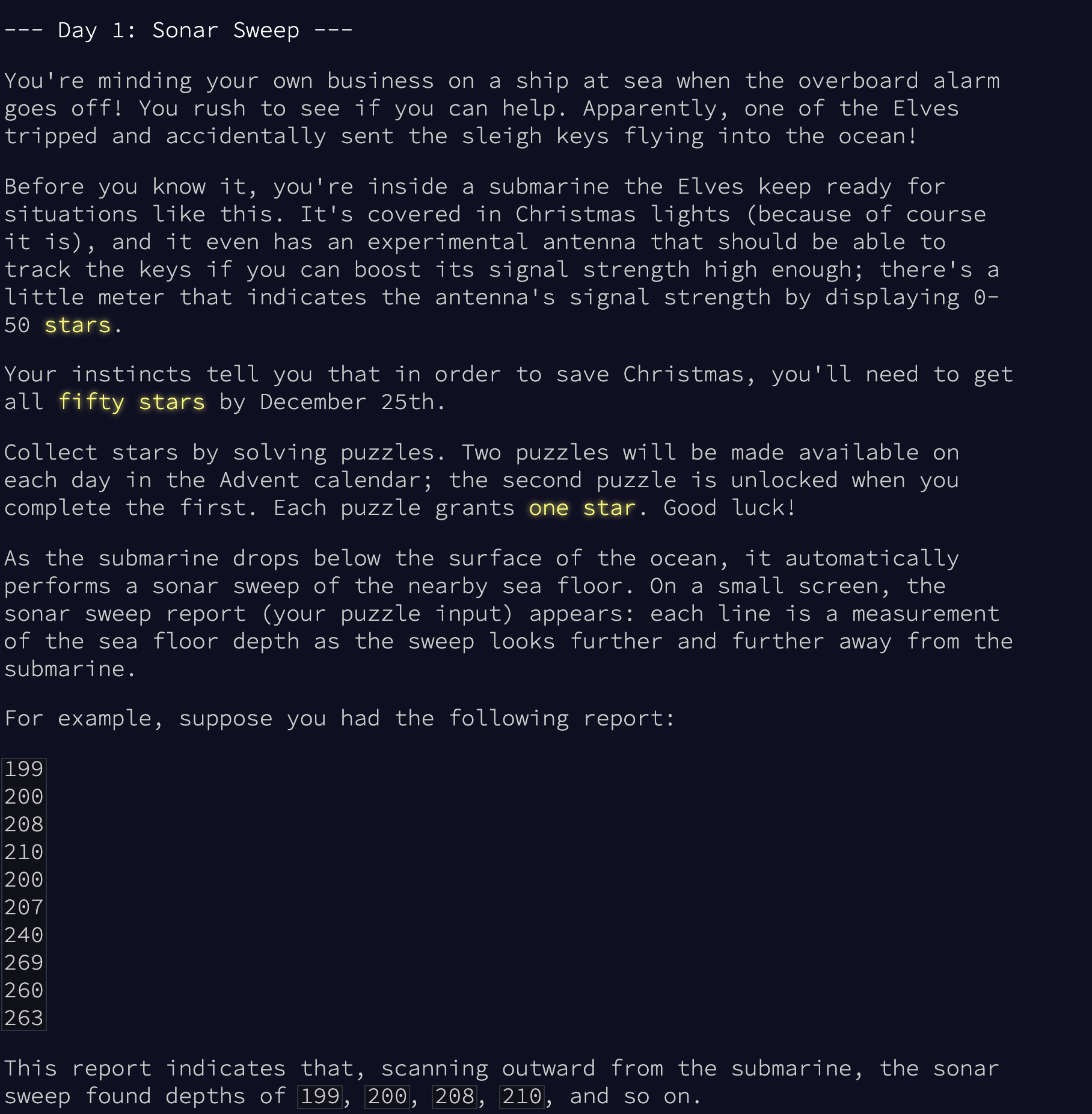
Here is the introduction provided in Problem 1. Most of this is simply the inception of the aformentioned storyline, and how to progress throughout the coding challenge, built upon in future problems. However, at the end, it begins to describe the first problem's requirements and a potential input file for the problem. Let's keep reading.
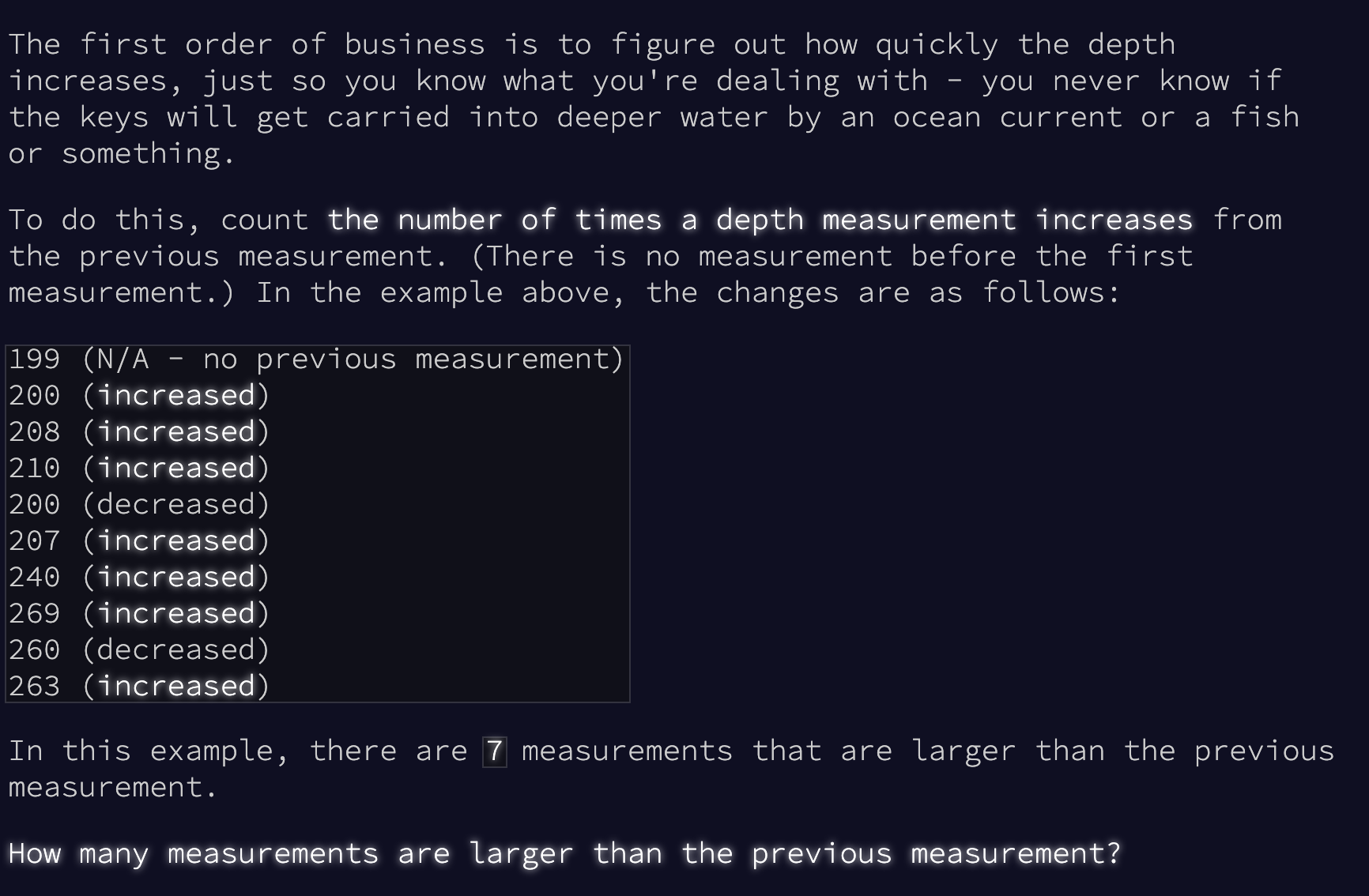
Now, given the description, we can simplify this problem into checking how many times a sequence of numbers is strictly increasing. I can't remember if the strictly piece of the equation actually came into play in the solution, Robbie if you remember to edit this markdown with if it did or not do so! If not let's assume it didn't unless I otherwise state in this blog post.
I now realize that I probably should've already mentioned I used Python for all my solutions. Syntax is relatively easy to follow, so even if you've never used it before you should be able to figure out what exaxctly my code is doing/trying to do. I really wish I had saved my work for this problem on Git (I am now!!) so I could refer to different versions or updates of my solution, however I will ultimately do my best at remembering how I solved the problem. The first important piece of the puzzle is, evidently, the input file. The input file represents the sequence of numbers we will be reading over. The input can be found here if you'd like to take a look yourself.
Problem Solution
My first order of business was getting the values in the input file into a python array. This could be done relatively easily in two lines of code:
file = open("sonarsweep.txt")
nums = file.readlines()Can be simplified to one line as such:
nums = open("sonarsweep.txt").readlines()open(param) takes an input file as parameter and makes its contents readable, and readlines() takes these contents, puts each individual line into an array, and returns that array. So, nums now contains an array of all the lines in our input file, where each line is a number in our sequence. Ultimately what this means is we now have an array representing our sequence of numbers. There are two key understandings we need to make about nums:
- Even though the input file is specific in its vales, we should write our code such that a similarly formatted file with different values can still be parsed in the same way. For instance, if I was to write a different input file still with numbers in each line, but the numbers were different, nums should still contain our desired sequence. Using the above blocks of code does this, and quite frankly is the most efficient way I know of doing it.
- All of the elements in nums are still strings. That's because even though all the values in our input file are numbers, readlines() pulls text in string form from the text files. We will need to typecast each of our values in the nums array to ints before doing any comparisons. This was a very common occurrence in most problems when parsing from text files, so if there are any issues with your code, make sure your variables are of the proper type.
Now it all comes down to looking through this array and seeing how many times the array is strictly increasing over the course of two elements. How can we do this? We can either do this process iteratively (use a for/while loop to check each individual element and then add to a running total) or recursively (recurse through the array where we add one to our output with each increasing element). I chose the iterative route, it's much easier to write and understand. Recursion is a very useful thought expriment, and I'll try my hand at some potential recursive code for this problem.
nums = open("sonarsweep.txt").readlines()
# Iterative Solution
def iter(n):
count = 0
for i in range(1, len(n)):
if int(n[i]) > int(n[i-1]):
count += 1
return count
print(iter(nums))
# Recursive Solution
def recur(n, i):
if i == len(n):
return 0
if int(n[i]) > int(n[i-1]):
return 1 + recur(n, i+1)
return recur(n, i+1)
print(recur(nums, 1))So I will admit that looking at my solution for this problem on GitHub will be much more of a clusterf*ck than looking at the above solutions. This is because after several rounds of debugging, I realized that some of the parsing from the input file to the nums array didn't go exactly as I had planned. However, for understanding the problem, we will assume that nums has parsed perfectly and we just have the elements from the text file.
Iterative Solution
Let's take a look at just the iterative solution above. If you're unfamiliar with Python syntax, def is a method declaration, with iter being the method name and nums being the parameter. So, we are creating a method iter with parameter n, which here can be any type. The only time we use this method, however, is the print statement where we pass our nums array in. So for the sake of simplicity, let's assume that the type of n whenever we see it is a string array.
We first initialize our counting variable to 0. Then, the foor loop syntax in the line
for i in range(1, len(n))is essentially saying "loop where i is equal to every value between 1 and the length of array n, including 1 but not including n." This is the equivalent as this for loop in java:
for (int i = 1; i < n.length; i++);The reason why we start at 1 will become clear in a second. So, inside our loop, we have an if statement where we finally make the comparison between two adjacenet elements in the array, at indeces i and i-1. If the element at index i is greater than that at index i-1, we increment count (count += 1). Otherwise, we continue on to the next iteration of the loop, or break out of it if we've reached the end of the array.
Now, do you see the reason we initalize i = 1? If we were to start at 0, we would compare indeces 0 and -1, which in Python actually compares the first and last elements (indexing in Python wraps around, so index -1 is the last element, -2 is the second to last element, etc.).
You may now be asking, "but Robbie, why does this if statement work?" We are trying to keep track of the amount of times an element in the array increases from the previous. In other words, how many times is an element greater than the last one? This is the question the if statement is asking. Tech Interview Tip: Try to understand, inspect and break down what exactly the question is asking and use that to guide your method of finding the result/output.
Recursive Solution
Finally, let's observe the code for the recursive solution. It's naturally going to be similar to the iterative solution in the sense that we are comapring element i and element i-1. The difference from the iterative solution is how we go about tracking what element in the array we are at. Since we don't have a for loop to set a range for the value, we store the index variable as a parameter in our recursive method along with the array. We will also need to write an if statement in our method which returns back to the original recursive call if we get to the end of the array. That is what the first if statement does:
if i == len(n):
return 0It might be confusing to see that we are returning 0 here. However, this does not mean that the whole problem is returning 0. 0 is only the result of this individual recursive call. Therefore, if we were to look at previous comparisons we made, those all added up will be our result. We add 1 to our running total by returning 1 plus the recursive call for the next element in the array, as such:
if int(n[i]) > int(n[i-1]):
return 1 + recur(n, i+1)
return recur(n, i+1)Finally, if our if statement does not evaluate true, and we want to continue checking elements, we do not add one to our running total, and just return the next recursive call. This can be seen in the line after the if statement above (this will only run if we do not return inside of the previous two if statements). Ultimately, after all elements are traversed, we get the same answer as our iterative solution.
Time & Space Complexity
Tech Interview Tip: It is crucial to be thinking about how modifications to how any changes or modifications to your solutions affects your runtime. That is ultimately what you are trying to do in a technical interview; display to the interviewer that you understand the ramifications of certain data structures or code modifications on overall runtime. It's okay in a lot of instances to not have a completely finished product; as long as you display that you know potential ways to optimize your solution, you'll do well wholesale.
Let's talk a bit about the runtime of our solution. As far as time is concerned, both the iterative and recursive solutions are going to run in O(n) time. What this means is that our runtime will be linear with respect to our input size, in this case the number of elements in our input file (which we put into the input array). We are looking at each element in the array once (One could argue twice if you consider we look back at another element, but our loop runs once through the array and that's what matters. Further, considering the previous element would mean we have O(n + n) = O(2n) runtime, which asymptotically evaluates to O(n)).
Space is a bit harder to put our hand on how precisely to evaluate it, however we can do so in each solution relative to each other. Both have the overhead of creating the new array, which we could potentially eliminate if we look at the input file directly. It's just a lot easier and nicer to understand by putting all the values into an array, and doesn't take up a significant amount of space overhead. The significance comes in the solution method. Our recursive solution creates a new method call for each element in the array, whereas iteratively we are only calling our method once. This means the recursive solution is significantly more expensive space-wise than the iterative solution. We are creating a new copy of our nums array, the iteration variable (i), and all of the code we wrote inside the method for each element in the array, rather than just once. This is why recursion is often inpractical if iteration can be written quicker. Some compilers, like the JVM, are capable of converting recursion to iteration to save that space overhead. However, it is often much more reliable and simpler to use iteration in practice.
So what now?
So if you somehow read through all that bullsh*t and made it out on the other side, congratulations. And thank you for reading through my post! I really appreciate it. I hope you learned something along the way or it helped you strengthen existing skills. The question now becomes what to do next. I would highly recommend looking through some of the other advent of code problems, which I will link again here. I cannot vouch for it enough, there are simply so many problems with different focuses and difficulties. I would consider this one of the easier problems, but it is still very useful in strengthening skills necessary for technical interviews. If you still have questions about my solutions here or my solution on GitHub, shoot me a PM on Discord or email and I'd be happy to talk it over! Same is true for Part 2 of this question, which (spoiler alert) is doing the same thing as Part 1 but for chunks of three consecutive values. Anyways guys, good luck on any technical interviews you have coming up, any Advent of Code problems you'll do in the future, Merry late Christmas, and take care!